概要
- SECCON CTF 14 予選で Team Enu は、グローバル 817 チーム中 34 位、日本国内では 6 位の成績を収めました。昨年に引き続き、今年も国内決勝へ進出します!
- 本記事では reversing ジャンルの
gyokuto問題を解説します。
はじめに
この記事は NFLaboratories Advent Calendar 20251 9 日目の記事です。
こんにちは、研究開発部の末廣です。弊社 NFLabs. は、情報セキュリティコンテストイベント SECCON2 のシルバースポンサーとして協賛しています3。
その SECCON の CTF イベント SECCON CTF 14 予選4 に、 NTT グループ有志と、募集5に応募いただいた学生の合同チーム Team Enu6 で参加しました。結果、グローバル 817 チーム中 34 位、日本国内では 6 位の成績を収めました。この順位は予選を突破して国内決勝へ進出できる順位です。 Team Enu は SECCON CTF 国内決勝へ 2 年連続出場します!
本記事では、筆者が貢献できた reversing ジャンルの gyokuto 問題を解説します。
gyokuto
amd64 ELF バイナリ gyokuto と、 78,400,000 バイトもある謎のファイル output.bin が与えられる問題です。解析結果の結論を先に書くと gyokuto バイナリが flag.txt ファイル内容を output.bin ファイルへ変換しているので、 output.bin から正解フラグを復元する内容です。
フラグを得る流れ
gyokuto バイナリを解析して output.bin ファイルの作られ方を解明
gyokuto バイナリを解析すると、 output.bin ファイルを次の内容で作成することが判明します。
- 「8 通りの周波数、 2 通りの位相をパラメーターとして、 200000 バイトの波形を生成する」関数を準備します。ここで周波数には 3-bit 分の擬似乱数値を使い、 1-bit 分の位相箇所にデータを使用します。
- まず 0, 1, 0, 1, 0, 1, 0, 1 の 8-bit 分の固定データそれぞれを位相として、合計 1600000 バイトの内容を得ます。この際 1-bit の擬似乱数値を生成しますが使いません。
- 次に
flag.txtファイル内容をビット単位へ分割し、各種 bit について擬似乱数値と排他的論理和を取った結果を位相として、 「ファイルサイズ * 8[bit] * 200000」 バイトの内容を追加していきます。 - 最終的な結果を
output.binファイルへ書き込みます。
gyokuto バイナリ内容をPythonコードで表現すると、次の内容になります。
import math # 擬似乱数生成器 class Prng: def __init__(self): # RVA 0x1E550 の関数で /dev/urandom ファイルから 16 バイト読み込み、 # RVA 0x1D650 の関数で 4 バイトずつに区切ってs0, s1, s2, s3とします。 # なお実際は、 RVA 0x1DAFC 付近の処理で、各種値が 0 の場合は代わりの固定値を使用します。その確率は 1 / (2**32) であり通常非該当であるため省略します。 self.s0 = s0 self.s1 = s1 self.s2 = s2 self.s3 = s3 def generate_next_bit(self) -> int: # RVA 0x1D4C0 の関数に、乱数生成処理が存在するようです。 # しかし本バイナリでは当該関数の呼び出しがインライン展開されているようで、直接本メソッド内容が埋め込まれています。 # たとえば RVA 0x19A49, 0x19F31, 0x1AC96, 0x1BC0A へ埋め込まれています。 xored = (self.s0 ^ (self.s0 << 11)) % 2**32 next_s3 = (self.s3 >> 19) ^ self.s3 ^ (xored >> 8) ^ xored self.s0 = self.s1 self.s1 = self.s2 self.s2 = self.s3 self.s3 = next_s3 return self.s3 & 1 # RVA 0x1B760 の関数です。詳細未解析です。内部的には別のPrngインスタンスを使用します。 def generate_noise() -> float: ... # RVA 0x1B0D0 の関数です。周波数と位相を引数に、ノイズ混ざり波形データを生成します。合計 100000 サンプル生成し、 1 サンプルあたり符号付き 16-bit 整数値を使用します。 def generate_wave_data(frequency: int, phase: int) -> bytearray: assert 0 <= frequency <= 7 assert 0 <= phase <= 1 result = bytearray() for i in range(100000): # 最初と最後は信号値を 0 にします。 100 個分かけて徐々に増減させます。 if i < 100: attenuation = i / 100.0 elif i >= 99900: attenuation = (100000.0 - i) / 100.0 else: attenuation = 1.0 signal = ( 0.125 * attenuation * math.cos( (frequency * 5000000.0 + 5000000.0) * 2 * math.pi * (i / 100000000.0) + (phase * math.pi) ) ) noise = generate_noise() # 平均 0 分散 0.01 の乱数を生成するようです。 # 実際はここで -2**31 <= value < 2**31 であるか確認する分岐があります。ほぼ確実に当該条件に当てはまるため、そうでない場合の分岐は省略します。 value = int((signal + noise) * 32767) result.append((value >> 0) & 0xFF) result.append((value >> 8) & 0xFF) return result def main(): # output.bin 書き込みまでのすべてが、 RVA 0x19010 の関数内容です。 with open("flag.txt", "rb") as fin: flag_data = fin.read() prng = Prng() output = bytearray() # 最初 8 データ分の phase は 01010101 の固定データです。 preamble 相当のようです。 for i in range(8): # MSB から 3-bit 分の擬似乱数を生成します。 frequency = sum(prng.generate_next_bit() << (2 - j) for j in range(3)) # 1-bit の擬似乱数を生成して捨てます。 prng.generate_next_bit() phase = i & 1 output.extend(generate_wave_data(frequency, phase)) # flag.txt 内容を MSB からビット単位に分割し、擬似乱数を XOR しつつ phase として使用します。 for i in range(len(flag_data)): for b in range(7, -1, -1): # MSB から 3-bit 分の擬似乱数を生成します。 frequency = sum(prng.generate_next_bit() << (2 - j) for j in range(3)) # ここで 1-bit の擬似乱数生成結果が関与していることが重要です。 phase = ((flag_data[i] >> b) & 1) ^ prng.generate_next_bit() output.extend(generate_wave_data(frequency, phase)) # RVA 0x1DC90 の関数内容です。 with open("output.bin", "wb") as fout: fout.write(output)
output.bin 内容から各波形の周波数 3-bit と位相 1-bitを解明
前述したように、 8 通りの周波数、 2 通りの位相をパラメーターとして、 200000 バイトの波形を生成します。ここで、パラメーターの種類は合計 16 パターンに限られます。実際に生成される各種波形にはノイズが加えられているものの、 16 パターンのうち最も近い波形を採用すれば、ノイズを除去できます。パターンが判明すれば、そのパターンで使用した周波数 3-bit と位相 1-bit も分かります。
判明した周波数情報から擬似乱数生成器の生成内容を復元し、位相情報を使ってフラグを入手
前述したように、波形生成時には擬似乱数生成器の生成結果を使います。
- 最初の8-bit 分の固定データ使用時は、ビットごとに、次の擬似乱数を生成、使用します。
- 周波数用に 3-bit 生成して使用。
- その後 1-bit 生成するも未使用。
- 続く
flag.txtファイル内容の各種ビット使用時は、次の擬似乱数を生成、使用します。- 周波数用に 3-bit 生成して使用。
- 位相用に、 1-bit 生成して、
flag.txtファイル内容のビットと XOR した値を使用。
つまりフラグを復元するためには、各波形の周波数および位相を解明するだけでは不十分であり、与えられる output.bin が生成されたときの擬似乱数生成器の生成結果も解明する必要があります。言い換えると、前述の Python コードにある class Prng 型 generate_next_bit メソッド呼び出し結果の戻り値のうち、 0-indexed として 4N 、 4N+1 、 4N+2 個目の生成結果が与えられるので、 4N+3 個目の生成結果を復元する必要があります。
さて、筆者は最初、 z37というライブラリを使って復元しようとしました。しかし筆者の使い方が悪かったのか、少なくとも数十分実行しても一向に計算が終わりませんでした。
解析状況をチームへ共有すると、チームメンバーが最後まで解いてくれました。16 パターンのうち最も近い波形の判定には、numpyライブラリの機能を活用しているようです。また、擬似乱数生成器の生成内容復元には、ガウスの消去法と呼ばれるアルゴリズムを使用しているようです。
#!/usr/bin/env python3 from __future__ import annotations import argparse import math import os from dataclasses import dataclass import numpy as np SAMPLES_PER_BIT = 100_000 BITS_PER_BYTE = 8 FREQ_CHOICES = 8 BITS_PER_PATTERN = 4 # xorshift next_bit() calls per segment @dataclass(frozen=True) class DecodeResult: freq_index: np.ndarray # (segments,), 0..7 phase_bit: np.ndarray # (segments,), 0/1 def default_output_path() -> str: # In this workspace the original challenge file is in extracted/output.bin # (the root output.bin may be overwritten during local experiments). if os.path.exists("extracted/output.bin"): return "extracted/output.bin" return "output.bin" def decode_freq_and_phase(output_path: str) -> DecodeResult: raw = np.memmap(output_path, dtype=np.int16, mode="r") if raw.size % SAMPLES_PER_BIT != 0: raise ValueError(f"unexpected sample count: {raw.size} (not multiple of {SAMPLES_PER_BIT})") segments = raw.size // SAMPLES_PER_BIT if segments % BITS_PER_BYTE != 0: raise ValueError(f"unexpected segment count: {segments} (not multiple of {BITS_PER_BYTE})") segs = raw.reshape((segments, SAMPLES_PER_BIT)) # Ignore attenuated edges (first/last 100 samples) and fold by period 20. start = 100 end = SAMPLES_PER_BIT - 100 window_len = end - start if window_len % 20 != 0: raise ValueError("internal error: window_len not multiple of 20") cycles = window_len // 20 r = np.arange(20, dtype=np.float64) ks = np.arange(1, FREQ_CHOICES + 1, dtype=np.float64).reshape(-1, 1) cos20 = np.cos(2.0 * math.pi * ks * r.reshape(1, -1) / 20.0) # (8, 20) freq_index = np.empty(segments, dtype=np.uint8) phase_bit = np.empty(segments, dtype=np.uint8) for i in range(segments): folded = segs[i, start:end].reshape((cycles, 20)).sum(axis=0).astype(np.float64) corr = cos20 @ folded # (8,) best = int(np.argmax(np.abs(corr))) freq_index[i] = best phase_bit[i] = int(corr[best] < 0.0) return DecodeResult(freq_index=freq_index, phase_bit=phase_bit) def xorshift128_lsb_masks(num_steps: int) -> list[int]: # Variables: 128 bits (s0,s1,s2,s3; each 32-bit word, LSB-first) s0 = [1 << b for b in range(32)] s1 = [1 << (32 + b) for b in range(32)] s2 = [1 << (64 + b) for b in range(32)] s3 = [1 << (96 + b) for b in range(32)] masks: list[int] = [] for _ in range(num_steps): xored = [0] * 32 for b in range(32): m = s0[b] if b >= 11: m ^= s0[b - 11] xored[b] = m xored_sr8 = [0] * 32 for b in range(24): xored_sr8[b] = xored[b + 8] s3_sr19 = [0] * 32 for b in range(13): s3_sr19[b] = s3[b + 19] new_s3 = [0] * 32 for b in range(32): new_s3[b] = s3[b] ^ s3_sr19[b] ^ xored[b] ^ xored_sr8[b] masks.append(new_s3[0]) # output bit after update s0, s1, s2, s3 = s1, s2, s3, new_s3 return masks def recover_xorshift128_state(freq_index: np.ndarray) -> tuple[int, int, int, int]: segments = int(freq_index.size) masks = xorshift128_lsb_masks(segments * BITS_PER_PATTERN) basis_mask = [0] * 128 basis_rhs = [0] * 128 def add_equation(row_mask: int, rhs: int) -> None: row = row_mask r = rhs & 1 while row: pivot = row.bit_length() - 1 if basis_mask[pivot]: row ^= basis_mask[pivot] r ^= basis_rhs[pivot] else: basis_mask[pivot] = row basis_rhs[pivot] = r return if r: raise ValueError("inconsistent constraints (bad decode?)") for i, f in enumerate(map(int, freq_index)): # PRNG outputs per segment: b3,b2,b1,b0 b3 = (f >> 2) & 1 b2 = (f >> 1) & 1 b1 = (f >> 0) & 1 add_equation(masks[BITS_PER_PATTERN * i + 0], b3) add_equation(masks[BITS_PER_PATTERN * i + 1], b2) add_equation(masks[BITS_PER_PATTERN * i + 2], b1) solution = 0 for pivot in range(128): if basis_mask[pivot] == 0: continue row = basis_mask[pivot] rhs = basis_rhs[pivot] parity = ((row & ~(1 << pivot)) & solution).bit_count() & 1 bit = rhs ^ parity if bit: solution |= 1 << pivot def extract_word(offset: int) -> int: v = 0 for b in range(32): if (solution >> (offset + b)) & 1: v |= 1 << b return v return (extract_word(0), extract_word(32), extract_word(64), extract_word(96)) def xorshift128_next_bit(state: list[int]) -> int: s0, s1, s2, s3 = state xored = (s0 ^ ((s0 << 11) & 0xFFFFFFFF)) & 0xFFFFFFFF ns3 = (s3 ^ (s3 >> 19) ^ xored ^ (xored >> 8)) & 0xFFFFFFFF state[0], state[1], state[2], state[3] = s1, s2, s3, ns3 return ns3 & 1 def recover_flag(output_path: str, *, verify: bool = True) -> str: decoded = decode_freq_and_phase(output_path) s0, s1, s2, s3 = recover_xorshift128_state(decoded.freq_index) # For the real flag region, the phase bit is XOR-masked with the 4th PRNG bit (b0). state = [s0, s1, s2, s3] b0 = np.empty(decoded.phase_bit.size, dtype=np.uint8) for i in range(decoded.phase_bit.size): xorshift128_next_bit(state) xorshift128_next_bit(state) xorshift128_next_bit(state) b0[i] = xorshift128_next_bit(state) bits = (decoded.phase_bit ^ b0).astype(np.uint8) byte_count = bits.size // BITS_PER_BYTE bits_msb = bits.reshape((byte_count, BITS_PER_BYTE)) weights = (1 << np.arange(7, -1, -1, dtype=np.uint8)).reshape((1, 8)) decoded_bytes = (bits_msb * weights).sum(axis=1).astype(np.uint8).tobytes() # The first byte is a preamble and is not masked by b0. flag_bytes = decoded_bytes[1:] if verify and not (flag_bytes.startswith(b"SECCON{") and flag_bytes.endswith(b"}")): raise ValueError("decoded bytes do not look like a SECCON{...} flag") return flag_bytes.decode("ascii") def main() -> None: ap = argparse.ArgumentParser(description="Solve SECCON CTF 'gyokuto' from output.bin") ap.add_argument("--input", default=default_output_path(), help="path to output.bin") ap.add_argument("--no-verify", action="store_true", help="skip SECCON{...} sanity check") args = ap.parse_args() print(recover_flag(args.input, verify=not args.no_verify)) if __name__ == "__main__": main()
実行すると、本問題のフラグ SECCON{R4bb1ts_h0p_0N_Th3_M00N_auRVXwxg5iIFJ0eM} を得られます。
バイナリの特徴や解決手段
さて、上では「gyokuto バイナリを解析すると」と簡単に表現しました。もしかしたら、バイナリ解析が簡単だったのでは、と思われた方もいるかもしれません。しかし実際は解析しづらい要素がいくつもあり、非常に骨が折れる内容でした。ここからはバイナリ解析時に苦労した内容を記述します。
Control Flow Flattening (CFF) による制御フロー難読化
Control Flow Flattening (CFF) とは、プログラムの流れを読みづらくする難読化手法の 1 つです。通常のバイナリでは、プログラミング言語でいうところの if による分岐や for によるループ構造が、基本的にはバイナリ中にそのまま表れます。分岐やループがない場所は上から下に一直線に処理が並びます。一方で CFF が施されたバイナリでは、各種処理が細かく分割され、かつ処理の順番が滅茶苦茶になるようにジャンプします。この CFF による難読化は、マルウェアでも使用される手法です。具体例は参考文献8をご参照ください。
例えば RVA 0x19010 の関数では、 CFF が施されていて関数内容が 66 個に分割されています。その関数の制御フローをグラフ表示したものが次の画像です。

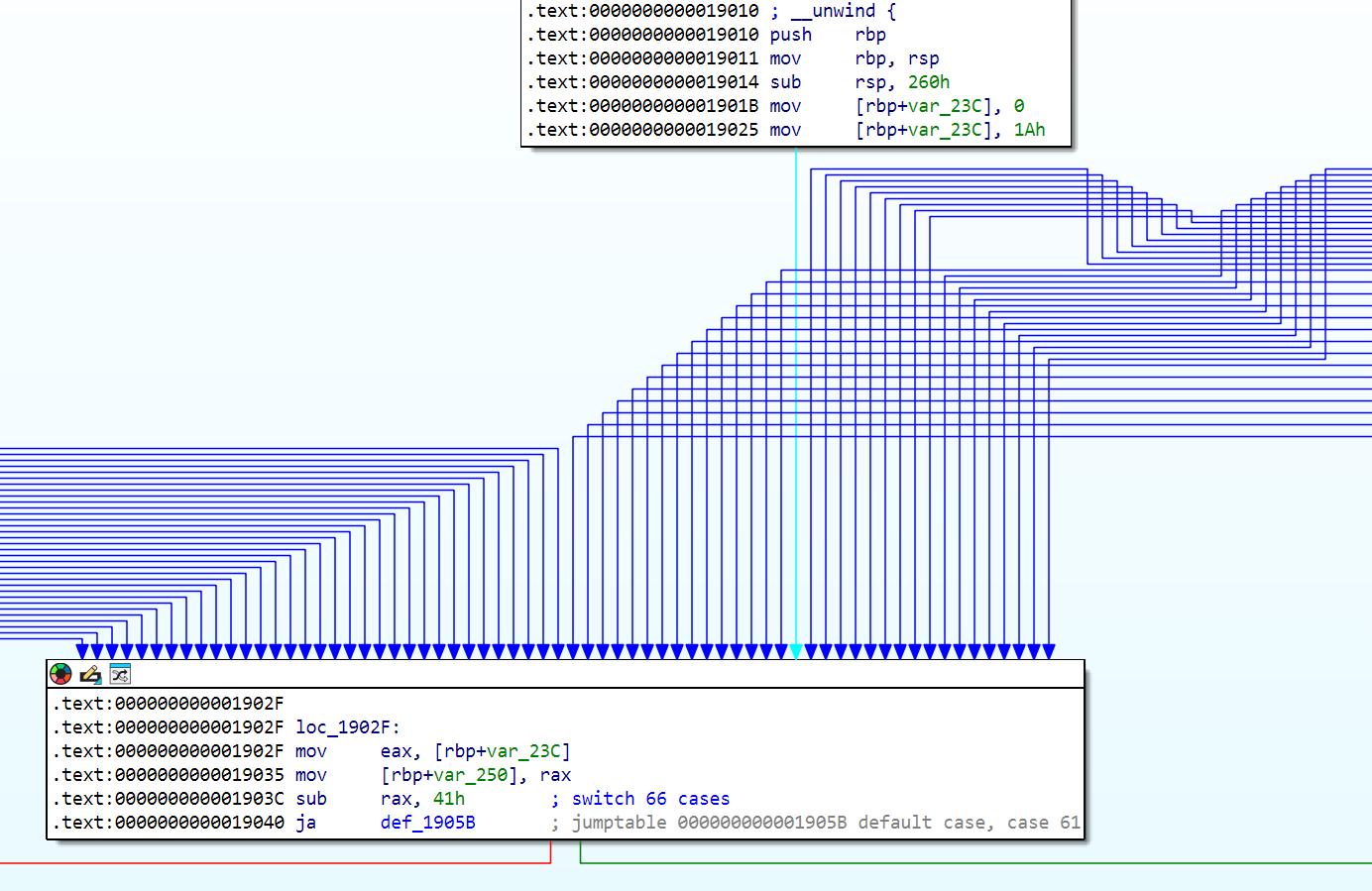
分割された処理のまとまりが横に並んでいるため、どの順番で処理が行われるのか、どこで分岐するのか等の理解が困難になっています。
例示した関数の逆コンパイル結果は、次のようになります。
v51 = 26; while ( 1 ) { v49 = v51; switch ( v51 ) { case 0u: *v122 = v111 + 1; v51 = 46; break; case 1u: sub_1B0D0((_QWORD *)v97, v67, v63); v132 = v70 + 1; *((_DWORD *)&v47 - 4) = v70 + 1 == v71; v35 = 51; if ( ((3 * (((unsigned __int8)(-36 - ((5 * *((_DWORD *)&v47 - 4) - 52) ^ 0xAC)) | 2) - 92)) & 1) != 0 ) v35 = 58; v51 = v35; break; // 同様に case が続きます。
上の例では switch ( v51 ) で処理内容が分岐していること、各種 case で v51 内容を更新して次の処理を決めていること、 case 1 の最後では *((_DWORD *)&v47 - 4) と複雑な計算を組み合わせて分岐先を決めていることが分かります。
解析時に最も苦労した点が、この CFF です。ただ幸いにして gyokuto バイナリにはデバッガー検知等が無いため、 gdb プログラムの dprintf9 機能を使って switch に使用される変数の値を出力することで、バイナリ実行中にどの case を通るのかを追跡しました。
dprintf 機能を使う際はアドレスが必要です。gdb 経由でのデバッグ時では通常 ASLR が無効化されているため、デバッグ対象バイナリのイメージベースは固定アドレスになります。通常ではイメージベースは 0x555555554000 になるようです。後はバイナリ解析で判明した RVA やレジスタの値を使って dprintf 機能のアドレスや文字列、表示内容等を組み立てて出力内容を制御します。
$ cat command.txt dprintf *(0x555555554000 + 0x19010), "sub_19010 begin\n" dprintf *(0x555555554000 + 0x19035), "sub_19010 case: %d\n", $eax run $ gdb -x command.txt ./gyokuto ... sub_19010 begin sub_19010 case: 26 sub_19010 case: 21 sub_19010 case: 6 ...
dprintf 機能の出力で判明した case 処理順序から、 CFF が施される前の本来のプログラム制御フローを考えていきました。
各種構造体の途中のアドレスを返す関数が多数存在
gyokuto バイナリでは 10 種類ほどのデータ構造を扱います。どうやらいずれのデータ構造でも参照カウント方式でインスタンスの寿命を管理しているようで、次のようなデータ構造となっています。
struct ReferenceCounterHeader { int shared_count; int size_and_tag; // 可変長配列等では上位 1 バイトがタグ。固定データ構造では全体がタグ。 }; struct VariableSizeString { ReferenceCounterHeader header; // tag には (size & 0xFFFFFFF) | 0x80000000 を格納します。 char string[]; // 可変長です。 }; struct VariableSizeUtf16String { ReferenceCounterHeader header; // tag には (size & 0xFFFFFFF) | 0x90000000 を格納します。 uint16_t string[]; // 可変長です。 }; struct Prng { ReferenceCounterHeader header; // tag には 0x200000 を格納します。 uint32_t state[4]; } // 他のデータ構造も、最初のメンバーは ReferenceCounterHeader 型メンバーです。
ここまでは何の変哲もないデータ構造ですが、gyokuto バイナリの特徴的な点として、構造体の途中のアドレスを返す関数が多数存在する点があります。例えば RVA 0x251D0 での、可変長文字列用データ構造を確保して返す関数は次の内容です。
VariableSizeString *__shifted(VariableSizeString,8) __fastcall InitializeVariableStringWithCapacity( int capacity_wihtout_null) { VariableSizeString *v1; // rax v1 = (VariableSizeString *)malloc(capacity_wihtout_null + 1 + 8LL); v1->header.shared_count = 1; v1->header.size_and_tag = capacityWithoutNull & 0xFFFFFFF | 0x80000000; v1->string[capacityWithoutNull] = 0; return (VariableSizeString *__shifted(VariableSizeString,8))v1->string; }
最後の return 箇所に着目すると、 malloc 結果の &v1 ではなく、 v1->string のアドレスを返していることが分かります。そのアドレスは、構造体先頭から 8 バイト進んだアドレスであり、参照カウント管理用ヘッダーを飛ばしたアドレスです。上記 RVA 0x251D0 関数の呼び出し元では、 v1->string メンバーだけではなく、マイナスのインデックスを突然使って参照カウント管理用ヘッダーを読み書きする箇所も多いため、解析時に面食らいます。
IDA では shifted pointer10 と呼ばれる機能があり、その機能を使うことで逆コンパイル結果を読みやすくできます。前述した、 InitializeVariableStringWithCapacity と命名している関数の戻り値の型 VariableSizeString *__shifted(VariableSizeString,8) が、 shifted pointer を使った型です。 shifted pointer で適切に型を付与している状態では、例えば RVA 0x1C140 付近の逆コンパイル結果は次の内容となり、十分読みやすくなります。
variable_string_flag_txt = InitializeVariableStringWithCapacity(9); strcpy(ADJ(variable_string_flag_txt)->string, "flag.txt"); variable_string_rb = InitializeVariableStringWithCapacity(3); strcpy(ADJ(variable_string_rb)->string, "rb"); variable_string_flag_txt_1 = ADJ(variable_string_flag_txt); shared_count = ADJ(variable_string_flag_txt)->header.shared_count; if ( shared_count > 0 ) variable_string_flag_txt_1->header.shared_count = shared_count + 1; size_flag_txt = ADJ(variable_string_flag_txt)->header.size_and_tag & 0xFFFFFFF;
また、型ごとに異なるタグが付与されている点は解析の助けになります。静的解析中にメンバーの型の辻褄が合わなくなって悩んだときに、動的解析でタグを確認すると、想定とは異なる型が使われていることが分かって間違いに気付いたこともあります。
複雑な浮動小数点数演算や SIMD 演算の存在
RVA 0x1D2F3 付近に、次の処理が存在します。
v7 = 0.7071067811865476; v8 = _mm_cmplt_sd((__m128d)*(unsigned __int64 *)&v19, *(__m128d *)&v7).m128d_f64[0]; v9 = COERCE_DOUBLE(~*(_QWORD *)&v8 & *(_QWORD *)&v19 | *(_QWORD *)&v8 & COERCE_UNSIGNED_INT64(2.0 * v19)) + -1.0; v7 = v9 / (v9 + 2.0) * (v9 / (v9 + 2.0)); v10 = (double)(v18 + (char)-(v19 < 0.7071067811865476)) * 0.6931471803691238 - (v9 * (v9 * 0.5) - ((double)(v18 + (char)-(v19 < 0.7071067811865476)) * 1.908214929270588e-10 + v9 / (v9 + 2.0) * (v9 * (v9 * 0.5) + v7 * v7 * (v7 * v7 * (v7 * v7 * 0.1531383769920937 + 0.2222219843214978) + 0.3999999999940942) + v7 * (v7 * v7 * (v7 * v7 * (v7 * v7 * 0.1479819860511659 + 0.1818357216161805) + 0.2857142874366239) + 0.6666666666666735))) - v9);
浮動小数点数の複雑な計算が行われています。加えて amd64 ELF では、浮動小数点数を xmm0 等の SIMD 用レジスタで扱うため、逆コンパイル結果でもしばしば SIMD 用命令がそのまま登場することになり、読解難易度が上がります。
今回は、複雑な処理を静的解析で理解することは諦めて、前述した dprintf 機能の出力から処理を推測しました。上述の RVA 0x1D2F3 を含む関数は、波形データを生成する関数から呼び出されます。波形データ生成箇所付近で、 dprintf 機能で計算結果を出力させました。
$ cat command.txt dprintf *(0x555555554000 + 0x1B43F), "%+08f, %+08f, ", $xmm0.v2_double[0], $xmm1.v2_double[0] dprintf *(0x555555554000 + 0x1B4A2), "%+016f, ", $xmm0.v2_double[0] dprintf *(0x555555554000 + 0x1B53C), "0x%04X\n", $ecx&0xFFFF run $ gdb -x command.txt ./gyokuto ... -0.030769, +0.000000, -00001008.200734, 0xFC10 +0.133050, +0.000000, +00004359.655771, 0x1107 -0.077218, -0.002500, -00002612.130205, 0xF5CC +0.050565, -0.000000, +00001656.865834, 0x0678 -0.033169, +0.005000, -00000923.014593, 0xFC65 +0.207748, +0.000000, +00006807.275358, 0x1A97 +0.105971, -0.007500, +00003226.598330, 0x0C9A +0.054596, -0.000000, +00001788.949024, 0x06FC +0.112900, +0.010000, +00004027.055880, 0x0FBB ...
左端の列が上述の RVA 0x1D2F3 を含む関数の戻り値であり、ランダムらしい値を計算していること(前述の Python 表現コードでの noise)が分かります。また他に出力している値では、左から 2 列目は周期的な値であり徐々に大きくなっていること(Python 表現コードでの signal)、左から 3 列目 や 4 列目は 1 列目の値と 2 列目の値の和が関係していそうなこと(前述の Python 表現コードでの value)が分かります。静的解析結果と dprintf による出力結果を合わせて、解析結果への自信を深めていきました。
遠回しな処理の存在
RVA 0x1F2E0 の関数は、タグが 0x200100 であるデータ構造を受け取ります。その型は関数ポインター型のメンバーを持ち、利用箇所すべてで RVA 0x1F0E0 の関数のアドレスを使用します。
RVA 0x1F2E0 の関数では、関数ポインター経由で RVA 0x1F0E0 の関数を呼び出したり、 RVA 0x1F0E0 の関数は CFF で内容が 8 分割されていたりするなど、理解できるまで時間のかかる内容でした。そして理解した結果が、タグが 0x200100 であるデータ構造の別のメンバーである可変長文字列データ構造を複製して返すという、一言で表現できる単純な内容でした。このように gyokuto バイナリでは、一見すると複雑な処理を行っているように見えて、実のところは単純な機能ということがありました。
コマンドライン引数を保持するも未使用
gyokuto バイナリの main 関数は最初に、 RVA 0x25FA0 の関数を argc および argv 引数で呼び出します。 RVA 0x25FA0 の関数は引数内容をグローバル変数へ保持します。
この流れから、コマンドライン引数もどこかで使われるものだと最初は思っていました。しかしグローバル変数の使用箇所は未使用関数だけであることが判明しました。つまり、コマンドライン引数は保持されるだけで、まったく使われません。
このことに確信を持てるまでは、 output.bin 生成内容に flag.txt だけではなくコマンドライン引数も関わる可能性を考える必要がありました。
mimalloc の静的リンクによるバイナリの肥大化
本内容は解析しづらさとは少し異なりますが、気付いた点として記述します。
gyokuto バイナリが動的メモリ確保に使用する malloc 関数や free 関数として、 glibc 標準のものではなく、静的リンクされた mimalloc11 ライブラリ内容を代わりに使用します。このことは、 gyokuto バイナリ中に含まれる文字列 cannot decommit OS memory から判明しました。
ライブラリが静的リンクされているため、 gyokuto バイナリ全体としてのコード量が増加しています。ただし gyokuto バイナリ中では、アプリケーションコード部分にはシンボル情報が無いため関数名は失われているものの、 malloc や free というシンボル名は残っています。そのため、アプリケーション部分から malloc 関数や free 関数を呼び出している箇所は明確であり、解析する立場では mimalloc ライブラリを使っていることはあまり影響がありませんでした。ライブラリの正体を調べるところや、 /dev/urandom 文字列の使用箇所が mimalloc 側で使われていたため前述した擬似乱数生成器と関係有無の調査に時間がかかったことぐらいの影響です。
おわりに
例年通り、今回の SECCON CTF でも挑戦しがいのある問題が多数出題されました。素晴らしいコンテストを開催くださった運営の皆様へ感謝を捧げます。
- https://adventar.org/calendars/11575↩
- https://www.seccon.jp/14/↩
- https://www.seccon.jp/14/seccon/sponsors.html↩
- https://www.seccon.jp/14/seccon_ctf/quals.html↩
- https://x.com/NFLaboratories/status/1988157951815938172↩
- https://team-enu.github.io/↩
- https://github.com/Z3Prover/z3↩
- https://news.sophos.com/en-us/2022/05/04/attacking-emotets-control-flow-flattening/↩
- https://sourceware.org/gdb/current/onlinedocs/gdb.html/Dynamic-Printf.html↩
- https://hex-rays.com/blog/igors-tip-of-the-week-54-shifted-pointers↩
- https://github.com/microsoft/mimalloc↩